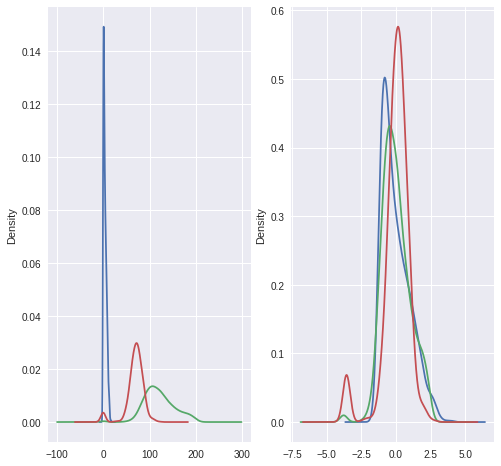
Standardization involves transforming dataset with Gaussian distribution to 0 mean and unit variance (standard deviation of 1).
Many learning algorithms assume that all features are centered around 0 and have variance in the same order
This recipe includes the following topics:
- Standarize using StandardScaler class
- Call fit() to compute the mean and std to be used for later scaling
- Call transform() on the input data
- Draw KDE plots to compare before and after Standardization
# import modules
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
# read data file from github
# dataframe: pimaDf
gitFileURL = 'https://raw.githubusercontent.com/andrewgurung/data-repository/master/pima-indians-diabetes.data.csv'
cols = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
pimaDf = pd.read_csv(gitFileURL, names = cols)
# convert into numpy array
pimaArr = pimaDf.values
# Though we won't be using the test set in this example
# Let's split our data into the usual train(X) and test(Y) set
X = pimaArr[:, 0:8]
Y = pimaArr[:, 8]
# 1. initiate StandardScaler class
# 2. call fit() to compute the mean and std
scaler = StandardScaler().fit(X)
# standarize input data using transform()
rescaledX = scaler.transform(X)
# limit precision to 3 decimal points for printing
np.set_printoptions(3)
# print first 3 rows of input data
print(X[:3,])
print('-'*60)
# print first 3 rows of output data
print(rescaledX[:3,])
# draw kde plot to see the transformation visually
# add two subplots
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(8, 8))
# plot KDE for input data
pimaDf['preg'].plot.kde(ax=ax1)
pimaDf['plas'].plot.kde(ax=ax1)
pimaDf['pres'].plot.kde(ax=ax1)
# convert rescaledX array to DataFrame
rescaledDf = pd.DataFrame(rescaledX, columns=['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age'])
# plot KDE for input data
rescaledDf['preg'].plot.kde(ax=ax2)
rescaledDf['plas'].plot.kde(ax=ax2)
rescaledDf['pres'].plot.kde(ax=ax2)
plt.show()of output data
print(rescaledX[:3,])
[[ 6. 148. 72. 35. 0. 33.6 0.627 50. ]
[ 1. 85. 66. 29. 0. 26.6 0.351 31. ]
[ 8. 183. 64. 0. 0. 23.3 0.672 32. ]]
------------------------------------------------------------
[[ 0.64 0.848 0.15 0.907 -0.693 0.204 0.468 1.426]
[-0.845 -1.123 -0.161 0.531 -0.693 -0.684 -0.365 -0.191]
[ 1.234 1.944 -0.264 -1.288 -0.693 -1.103 0.604 -0.106]]